
Stacks in Python
Introduction
A stack is a linear data structure that follows the Last-In-First-Out (LIFO) principle. Think of it like a stack of plates: you can only add or remove plates from the top.
Key Operations in stacks:
- Push: Add an element to the top of the stack.
- Pop: Remove the top element from the stack.
- Peek: View the top element without removing it.
- isEmpty: Check if the stack is empty.
Stacks in python are a dynamic data structure as they can grow (with increase in number of elements) or shrink (with decrease in number of elements). A static data structure, on the other hand, is the one that has fixed size.
Stack: The Data Structure
In this section “Stacks in Python“, we will provide a comprehensive introduction to all useful concepts about stacks in python which are used in programing with examples including the following topics
- What are stacks in python
- Example of stack operations in Python
- How to implment stacks in Python
- Applications of stacks in Python
- Algorithms of stacks in python
And, by the end of this tutorial, you will have a solid understanding of all about stack data structure in Python like Application of stacks, Algoritms of stacks and Implementation of stack using python and will be able to use this knowledge in their own python programming projects.
Also this tutorial covers all necessary topics/concepts required to complete your exams preparations in CBSE schools / classes 11th and 12th.

A stack is a linear structures implemented in LIFO (Last In First Out) manner where insertions and deletions are restricted to occur only at one end – stack’ s top. LIFO means element last inserted would be the first one to be deleted. Thus, we can say that a stack is a list of data that follows these rules:
- Data can only be removed from the top (pop), i.e., the element at the top of the stack. The removal of element from a stack is technically called POP operation.
- A new data element can only be added to the top of the stack (push). The insertion of element in a stack is technically called PUSH operation
Consider figure below that illustrates the operations (push and pop) on a stack.
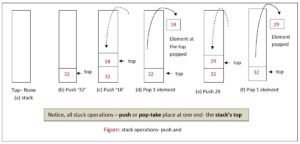
Some Other Stack Terms in python
There are some other terms related to stacks, such as peek, overflow and Underflow.

Peek:
Refers to inspecting the value at the stack’s top without removing it; it is also sometimes referred as inspection.
Overflow:
Refers to situation (ERROR) when one tries to push an item in stack that is full. This situation occurs when the size of the stack is fixed and cannot grow further or there is no memory left to accommodate new item.
Underflow:
Refers to situation (ERROR) when one tries to pop/ delete an item from an empty stack. That is, stack is currently having no item and still one tries to pop an item. Consider some examples illustrating stack-functioning in limited- size stack. (Please note, we have bound fixed the capacity of the stack for understanding purposes.)
Operations in stacks in python: PUSH and POP
Let’s have an example of a bounded stack of capacity 4 which is initially empty, and drawing pictures of the stack after each of the following steps. Initially the stack is empty.
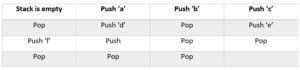
Solution.
- Stack is empty (top = None )
- Push ‘a’ top = 0
- Push ‘b’ top = 1
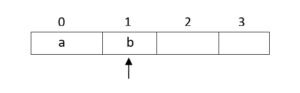
- Push ‘c’ top = 2
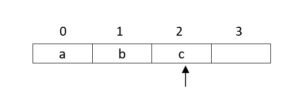
- pop top = 1
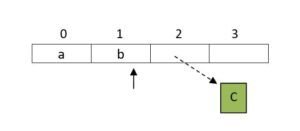
- push ‘d’ top = 2
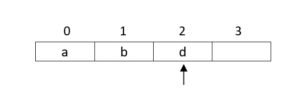
- pop ‘d’ top = 1
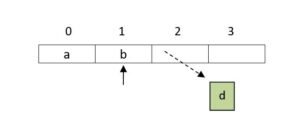
- Push ‘e’ top = 2
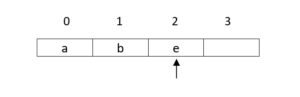
- Push ‘f’ top = 3
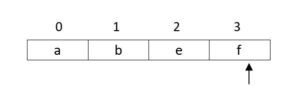
- Push ‘g’ top = 3
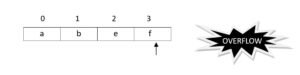
[OVERFLOW because the stack is bounded, it cannot grow. If it could grow, then there would have been no OVERFLOW until no memory is left.
In python, (for stacks implemented through lists) since lists can grow, OVERFLOW condition does not arise until all the memory is exhausted.]
- Pop top = 2
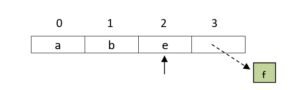
- pop top = 1
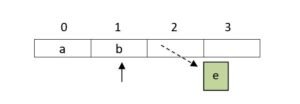
- pop top = 0
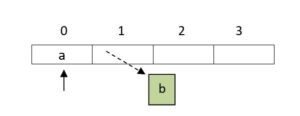
- pop top = none
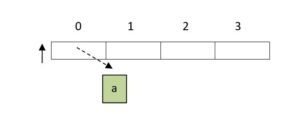
- Push top = none

Implementing stacks in python
In python, you can use lists to implement stacks. Python offers us a convenient set of methods to operate lists as stacks.
For various stack operations, we can use a list say stack and use python code as described below:
Peek we can use: <stack> [top]
where < stack> is a list; top is an integer having value equal to len (<stack>) -1.
Push we can use: <stack>. append (<item>)
when <item> is the item being pushed in the stack.
Pop we can use: <stack>. Pop ( )
it removes the last value from the stack and returns it.
Let us now implement a stack of through a program.
def push (stk, item):
Program Code:
Python program to implement stack operations.
STACK IMPLEMENTATION
“ “ “
Stack: implemented as a list
top: integer having position o topmost element in stack“ “ “
def is Empty (stk):
if stk == [ ]
return True
else:
returns False
def push (stk, item) :
stk. append (item)
top = len (stk) -1
def pop (stk):
if is Empty (stk) :
return “underflow”
else:
item = stk. Pop ( )
if len (stk) == 0:
top = None
else:
top = len (stk) -1
return item
def peek (stk) :
if is Empty (stk) :
return “underflow”
else:
top = len (stk) -1
return stk [top]
def Display (stk) :
if is Empty (stk) :
print (:stack empty”)
else:
top = len (stk) -1
print (stk[top], “<- top” )
for a in range (top- 1, -1, -1 ) :
print (stk [a])
#_main_
stack = [ ] # initially stack is empty
top = None
While True:
print (“STACK OPERATIONS”)
print (“1. Push”)
print (“2. Pop”)
print (“3. Peek”)
print (“4. Display stack”)
print ( “5. Exit”)
ch = int (input (“Enter your choice (1-5) :” ) )
if ch == 1 :
item = int (input (“Enter item:” ) )
push (stack, item)
elif ch == 2 :
item = pop (stack)
if item ==”underflow”
print (“underflow” : stack is empty !” )
else:
print (“popped item is”, item)
elif ch == 3:
item = peek (stack)
if item ==”underflow”
print (“underflow! Stack is empty!”)
else:
print (“Topmost item is”, item)
elif ch == 4:
Display (stack)
elif ch == 5:
break
else:
print (“Invalid choice!” )
Sample run of the above program is as shown below:

Types of Stacks – Itemnodes in python
An item stored in a stack is also called item- node sometimes. In the above implemented stack, the stack contained item-nodes containing just integers. If you want to create stack that may contain logically group information such as member details like: member no, member name, age etc. For such the item-node will be a list containing the member details and then this list will be entered as an item to the stack. (See figure below)
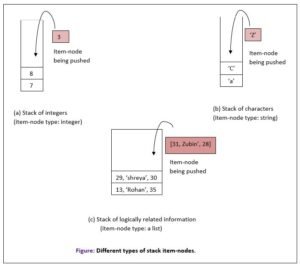
- For stack of figure (a), the stack will be implemented as stack of integers as item-node is of integer type.
- For stack of figure (b), the stack will be implemented as stack of strings as item-node is of string type.
- For stack of figure (c), the stack will be implemented as stack of lists as item-node is of list type. Solved problem 20 implements such a s
Applications of Stacks in python
There are several applications and uses of stacks. The stacks are basically applied where LIFO (Last in First Out) scheme is required
Reversing a line using stacks in python
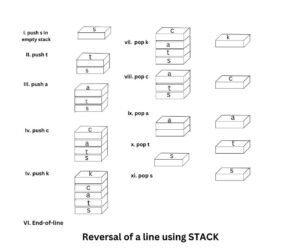
A simple example of stack application is reversal of a given line. We can accomplish this task by pushing each character on to a stack as it is read. When the line is finished, characters are then popped off the stack, and they will come off in the reverse order as shown in Figure below. The given line is: Stack.
Polish Strings using stacks in python
Another application of stacks is in the conversion of arithmetic expressions in high-level programming language into machine readable form. As our computer system can only understand and work on a binary language, it assumes that an arithmetic operation can take place in two operands only e.g., A+ b, c D, D/A etc. But in our usual from an arithmetic expression may consist of more than one operator and two operands
For example:
(A + B) C (D/(J + D)).
These complex arithmetic operations can be converted into polish string using stacks which then can be executed in two operands and a operator form.
Polish string, named after a polish mathematician, Jan Lukasiewicz, refers to the notation in which the operator symbol is placed either before its operands (prefix notation) or after its operands (postfix notation) in contrast to usual form where operator is placed in between the operands (infix notation).
Following table shows the three types of notations:

Conversion of infix Expression to Postfix (Suffix) Expression
While evaluating an infix expression, there is an evaluation order according to which
I Brackets or Parenthesis,
II Exponentiation,
III Multiplication or Division,
IV Addition or Subtraction
Take place in the above specified order. The operators with the same priority (e.g., and/) are evaluated from left to right.
To convert an infix expression into a postfix expression, this evaluation order is taken into consideration.
An infix expression may be converted into postfix from either manually or using a stack. The manual conversion requires two passes: one for inserting braces and another for conversion. However, the convert an infix expression into a postfix expression manually are given below:
- Determine the actual evaluation order by inserting branches.
- Convert the expression in the innermost branches into postfix notation by putting the operator after the operands.
- Repeat step (ii) until entire expression is converted into postfix notation.
Example: Convert (A+B) × C /D into postfix notation.
Solution:
Step 1: Determine the actual evaluation order by putting braces
=((A+B)×C)/D
Step 2: Converting expressions into innermost braces
=((AB+)×C)/D=(AB+C×) / D = AB +C × D /
Example: Convert((A+B)*C / D + E^F)) / G into postfix will be
=((((AB+B) *C) / D) +(E^F))/G
Converting expressions in the braces, we get
=((((AB+) *C)/D) + (EF^))/G
=(((AB+C*)/D) + EF^)/G
=((AB+C*D/) +EF^)/G= (AB + C * D/EF ^ +)/G
=AB + C * D/EF ^ +G/
Example: Give postfix from of the following expression
A* (B+(C+D) * (E+F)/*H
Solution: Evaluation order is
(A*(B+((C+D) * (E+F))/G)) *H
Converting expression in the braces, we get
=(A*(B+[(CD+) *(EF+)]/G)) *H=A*(B+ (CD+EF+ *)/G) * H
=A* (B+(CD+EF+ *G/)) * H=(A* (BCD + EF + *G/+))* H
=(ABCD+EF + *G/ + H = ABCD +EF +*G/+ *H*
Example: Give postfix from for A+[(B+C) + (D+E) * F]/G
Solution:
Evaluation order is: A +[{(B+C) + ((D+E) * F)}/G
Converting expressions in braces, we get
=A + [{(BC +) + (DE+) * F}/G] = A+ [{(BC +) + (DE + F *)}/G]
=A + [{BC + DE +F * +}/G] = A + [BC +DE +F * +G/]
=ABC +DE +F * +G / +
Example: Give postfix form of expression for the following: NOT A FOR NOT B NOT C
Solution:
The order of evaluation will be
((NOT A) OR ((NOT B) AND (NOT C)))
(As priority order of NOT, AND, OR)
= ((A NOT) OR ((B NOT) AND (C NOT)))
= ((A NOT) OR ((B NOT C NOT AND))
= A NOT B NOT C NOT AND OR
While converting from infix to prefix form, operation are put before the operands. Rest of the conversion procedure is similar to that of infix to postfix conversion.
Algorithm to convert infix Expression to postfix form
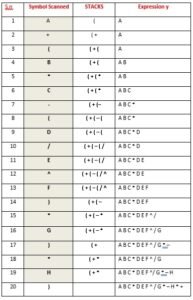
The following algorithm transforms the infix expression X into its equivalent postfix expression Y. The algorithm uses a stack to temporarily hold operators and left parentheses. The postfix expression Y will be constructed from left to right using the operands from X and the operators which are removed from STACK. We begin by pushing a left parenthesis onto STACKS and adding a right parenthesis at the end of X. The algorithm is completed when STACKS is empty.
Algorithm for Infix to postfix conversion using stacks in python
Suppose X is an arithmetic expression written in infix notation. This algorithm finds the equivalent postfix expression Y.
- Push “(“onto STACKS, and add “)“ to the end of X.
- Scan X from left to right and REPEAEAT Steps 3 to 6 for each element of X until the STACKS is empty:
- If an operand is encountered, add it to Y.
- If a left operand is encountered, push it onto STACKS.
- If an operator is encountered, then:
- Repeatedly pop from STACKS and add to Y each operator (on the top of STACKS) Which has the same precedence as or higher precedence than opera.
- Add operator to STACKS.
‘ ‘ ‘ End of if structure’ ‘ ‘
- If a right parenthesis is encountered, then:
- Repeatedly pop from STACK and add to Y each operator (on the top of STACK) until a left parenthesis is encountered.
- Remove the left parenthesis. [Do not add the left parenthesis to Y].
‘ ‘ ‘ End of if structure’ ‘ ‘
‘ ‘ ‘ End of step 2 Loop’ ‘ ‘
- END
Solution:
Evaluation of a postfix Expression using stacks in python
As postfix expression is without parenthesis and can be evaluated as two operands and an operator at a time, this becomes easier for the compiler and the computer to handle. Evaluation rule of a postfix expression states:
- While reading the expression from left to right, push the element in the stack if it is an operand;
- Pop the two operands from the stacks, if the element is a binary operator. In case of NOT operator, pop one operand from the stack and then evaluate it (two operands and an operator).
- Push back the result of the evalution. Repeat it till the end of the expression.
For a binary operator, two operands one popped from stack and for a unary operator, one operand is popped. Then, the result is calculated using operand(s) and the operator, and pushed back into the stack.
Algorithm Evaluation of postfix expression
‘‘‘Reading of expression takes place from left to right ‘‘‘
- Read the next element ‘ ‘ ‘first element for the first time’ ‘ ‘
- If element is operand then
Push the element in the stack
- If element is operator then
{
- Pop two operands from the stack
‘ ‘ ‘pop one operand in case of unary operator’ ‘ ‘
- Evaluate the expression formed by the two operands and the operator
- Push the result of the expression in the stack end
}
- If no-more-elements then
Pop the result
Else
Go to step 1.
- END
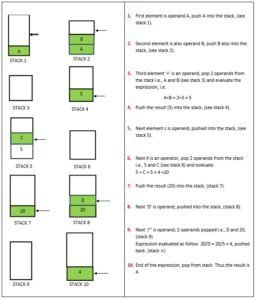
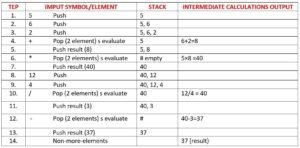
Example: Evaluation the postfix expression AB + C × D / IF A =2, B =3, C =4 and D =5.
Solution. The expression given is AB + C × D/
Starting from left to right
Evaluation of prefix expression using stacks in python
The prefix expression is also without parentheses. The prefix expression are evaluated by the compiler by using two stacks:
- One stack (symbol stack) for holding the symbols of the expression (all the operators and operands/values of the expression are considered symbols) and
- Another stack (number stack or operand-value stack) for holding the numbers
- numbers or values (i.e., the operands).
Example: Evaluated the expression 562 + * 124 /- in tabular form showing stack status every step.
Advantage of postfix Expression over infix Expression in python
An infix expression is difficult for the machine to know and keep track of precedence of operators. On the other hand, a postfix expression itself determines the precedence of operators (as the placement of operators in a postfix expression depends upon its precedence). Therefore, for the machine it is easier to carry out a postfix expression than an infix expression.


