Recursion in Python | CBSE Class 12

What is Recursion in Python

Recursion in Python is a programming technique in which a function calls itself directly or indirectly. It’s a very simple way to solve problems that can be broken down into smaller, similar sub problems.

Example: Calculating Factorial

def factorial(n):
if n == 0: # Base case
return 1
else: # Recursive case
return n * factorial(n – 1)

print(factorial(5))

 

 

Introduction

In this section “Recursion in Python“, we will provide a comprehensive introduction to all useful concepts about recursion and recursive functions in python which are used in programing with examples including the following topics

And, by the end of this tutorial, you will have a solid understanding of all about Recursion and important recursive function in Python and will be able to use this knowledge in their own python programming projects.

Also this tutorial covers all necessary topics/concepts required to complete your exams preparations in CBSE schools / classes 11th and 12th.

 

We have learnt how to create and invoke methods / functions in python *Read Here(. Inside the function bodies, we can include function – calls of other functions. But have you ever thought: could a method invoke or call itself?

Self – invocation may at first sound useless or illegal: Isn’t this defining something in terms of itself- what is called a circular definition? But self-invocation is legal, and it’s actually quite useful. In fact, it’s so useful that it gets its own special name: recursion.

Introduction to Recursion/recursive function in python

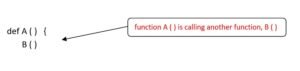
In many of your programs, you must have written some functions call or invoke other functions, examples:

Now, if you write a function definition that calls itself, then this function would be known as recursive function.

See, another recursive function:

                   def recur ( ):
                          recur ( )                             # calling itself

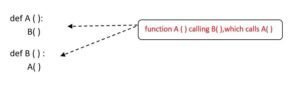
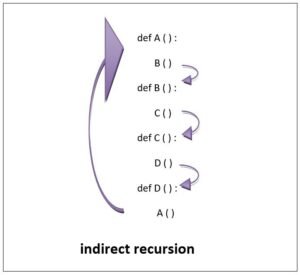
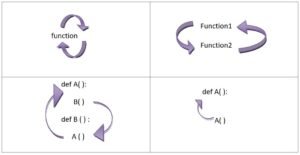
Recursion can be indirect also. The above example, where a function calls itself directly from within its body is an example of direct recursion. However, if a function calls another function which calls its caller function from within its body, it is known as indirect recursion example:

So, we can say that recursion can be of the following types:

Direct recursion:

if a function calls itself directly from is function body.

Indirect recursion:

if a function calls another function, which calls its caller function.

Following figure illustrates it.

Examples of indirect recursion in python        

The above shown sample code is an example of indirect recursion.

In mathematics also, you have seen recursive problems e.g., sum of n natural numbers can be written as

and so on.

Now, We shall be learning how to write recursive function and implement recursion. But before we proceed, carefully go through the following code and figure out its output.

def fn1 ( )
      print (“Hello func2”)
      func2 ( )

def func2 ( )
     print (“yes func1” )
     func1 ( )

Yes, you guessed it right. This code will print the following ENDLESSLY:

Hello func2
Yes func1
Hello func2
Yes func1

      ..

      ..

      ..

The above functions (fun1 ( ) and func2 ( )) will keep on calling one another infinitely and the entire memory will be used up – Non stop! and Python will report following runtime error for it:

Runtime Error: maximum recursion depth  exceeded . . .

The problem with above code is that it is a Recursive program but recursion code is NOT SENSIBLE. You must write a sensible recursive code that has clearly defined ‘where to stop’. Let us see how.

Right or sensible Recursive code is the one that fulfills following requirements:

• It must have a case, whose result is known or computed without any recursive calling- the BASE CASE. The BASE CASE must be reachable for some argument/ parameter.
• It also have Recursive case, where by function calls itself later section, (section 6.4, explains this clearly.

To understand the above points, let us consider an example of python program first and see how it works.

python code example of recursion in python 

write a recursive function that computes the sum of numbers 1..n; get the value of last number n from user.

The output produced by above code is:

The sum of the series from 1..4 is 10

 

Let us now understand how it works. lines 3-7 of above program define a function compute( ),

which is a recursive function as it calls on line 7.

1. Program starts _ main_ part at line 9 and then calls compute (4) with variable last that has value 4, i.e., compute (4) is invoked at line 11 initially.
2. With function call compute (4) at line 11, control shifts to line 3, where the code of compute ( ) begins; parameter num takes value 4.
   • At line 4, condition num ==1 is false, so control shifts to else part (line 6-7).
   • Line 7 calculates return value as num + compute (num-1), as 4 = computer (4-1), i.e., 4) compute (3).
     

since the value of compute (3) is not known, function compute ( ) is to be called with value 3.

So compute ( ) is again called with value 3 so num takes value In line 4, num (which is 3) is still not 1 (condition 3 ==1 is false, ) so line 7 (its return value) gets computed as 3 + compute (3-1) i.e., 3+ compute (2)

for compute (2), line 4 condition num ==1 is false (as num is 2) so line 7(its return    value) is executed as 2 + compute (1)

for compute (1) condition of line 4 (num ==1) is true as num is 1 now. So compute (1) returns value 1 as line 5 gets  executed and control returns to 2+compute (1) (2.2.1.1A) with value 1 for compute (1).

so after returning to 2.2.1.1.A, the compute (2),s return value is calculated as 2+ compute (1) =2 +1= 3(value of compute (1) is 1). It calculates the compute (2)’s return value as 3. So the control returns to 2.2.1.

compute (2) returns value 3. So return of 3 gets computed as 3+ compute (2) = 3+ 3 = 6. Now the control returns to 2.2.

compute(3) returns 6 and thus the return value of compute (4) gets computed as 4+6 = 10 and control returns to line 11 that called computed (4) as ssum = compute(4)

3. Now variable ssum gets the return value of compute (4) as 10 and then at line 12, it prints the sum.

What this program manages to do is to display the value of 4+ (3+ (2+ 1 ). That is, it displays the sum of the numbers from 4 down to 1. More generally, what compute method does is to return the sum of all the integers between 1 and its parameter n.

How Recursion in python works?

Did you notice that the compute function doesn’t’ always recur: when its parameter n is 1, the function simply returns immediately without any recursive invocations. (line5)

With a bit of thought, you’ll realize that any functional recursive function must have such a situation, since otherwise, the recursive function will never finish. In fact, these situations are important enough to designate special case (s) where result is pre-known without invoking the function again: Any condition where a recursive function does not invoke itself is called a base case.

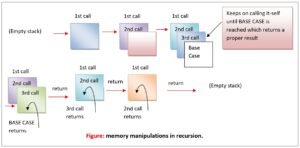
But what exactly happens when a recursive function lacks a base case? To understand this, we need to get some idea about how a computer- handles function invocations.

In executing a program, the computer creates what is called the function stack. The function stack is a stack of frames, each frame corresponding to a function invocation. At all times, the computer works on executing whichever function is at the stack’s top; but when there is a function invocation, the computer creates a new frame and places it atop the stack. When the function at the stack’ s top returns, the computer removes that function’ s frame from the stack’s top, and resumes its work on the function now on the frame’s top.

To see how this works, let’s  have previously given program’s diagram and see how it operated.

How recursion works: Step 1

How recursion works: Step 2

How recursion works: Step 3

How recursion works: Step 4

How recursion works: Step 5

How recursion works: Step 6

How recursion works: Step 7

How recursion works: Step 8

How recursion works: Step 9

How recursion works: Step 10

And after this, the program ends its frame is also removed from stack and stack becomes empty

So we can say that above given compute (4) was executed as follows:

Compute (4)

= 4 + compute (3)

= 4 + ( + compute (2) )

= 4 + (3 + (2 + compute (1) ) )

= 4 + (3 + (2 + 1 ) )

= 4 + (3 + 3 )

= 4 + 6

= 10

 

Some Example of recursion are given below for your better understanding

Python Code example 1

write a recursive function to print a string backwards.

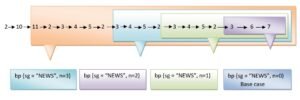
1.  # simple recursion
2. def bp (sg, n ):
3. If n > 0 :
4. Print (sg [n], end = ‘ ’)
5. Bp (sg, n-1 )                                       #recursive call to function bp ( )
6. Elif n = =0 :
7. Print (sg [0] )
9.  #_main_
10. S = input (“Enter a string : “)
11. bp (s, Len(s) – 1)

 

The output produced by above program is as shown below:

Enter a string : NEWS
SWEN

Can you figure out the flow of execution of above program? It is:

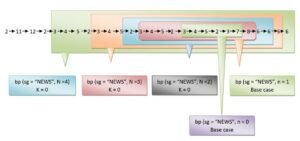
Consider another recursive function that also does the same thing as above previous program, backward printing of string.

Python Code example 2

write a recursive function to print a string backwards.

The output produced by above program is as shown below:

Enter a string   :   NEWS

SWEN

Can you figure out the flow of execution of above program? It is:

Thus, as you can see that flow of execution of above program is as :

Technically, python arranges the memory spaces needed for each function call in a stack. The memory area for each new call is placed on the top of the stack, and then taken off again when the execution of the call is completed. So, you can say that, the stack goes through the following sequence in recursive calls:

Python uses this stacking principal for all nested function calls – not just for recursively- defined functions. A stack is an example of a “last in / first out” structure

Now, You are ready to move to python programming for handling repetitive tasks using your coding skill. Let’s do it now.

 Recursion in Python

As you have seen, recursion occurs when a function calls itself. In python, as in other programming languages that support it, recursion is used as a form of repetition that does not involve iteration.

A Recursive Definition is a definition that is made in terms of a smaller version of itself. Have a look at following definition of x”, which is non – recursive:

^Xn = x* x*….* x                           (Iterative definition– nonrecursive) 

Now, it can be represented in terms of recursive definition as follows:

Xⁿ = x* (x ^n-1 )       for n > 1         (Recursive definition)

= x                        for n = 1

= 1                       for n = 0  

Writing a Recursive function. Before you start working recursive function, you must know that every recursive function must have at least two cases:

 

• The Recursive case ( or the inductive case )
• The Base case (or the stopping case)-ALWAYS REQUIRED

 

The Recursive case is the more general case of the problem we’re trying to solve using recursive call to same function.

The Base Case is small problem that we known how to solve and is the case that causes the recursion to end. In other words, it is the case whose solution is pre- known (either as a value or formula ) and used directly

As an example, with the power function xⁿ , the recursive case would be:

Power (x, n ) = x* power (x, n-1)

and the base case would be

Power (x, n) = x when n = 1

and         

Power(x, n) = 1 when n = 0

Other cases (when n< 0) we are ignoring for now for simplicity sake.

Consider the following example (program 6.4) of power function:

 

Python Code example

program to show the use of recursion in calculation of power like  a^b

# power a to using recursion 6_4

def power (a,b ) :

        If b = = 0 :                         #BASE CASE

                 return 1

           else :

                return a * power (a, b-1 )

#_main_

Print (“Enter only the positive numbers below” )
num = int ( input (“ Enter base number :” ) )
p = int (input ( “raised to the power of :” ) )
result = power (num, p )
print (num, “raised to the power of” , “is” , result

The output produced by above program is as :

Enter only the positive numbers below
Enter base number: 7
raised to the power of: 3
7 raised to the power of 3 is 343 

If there is no base case, or if the base case is never executed, an infinite recursion occurs. An infinite Recursion is when a recursive function calls itself endlessly. Infinite recursion can happen in one of the following cases.

1. Base Case Not Defined. When the recursive function has no BASE CASE defined, infinite recursion will occur.
2. Base Case Not reached. Sometimes you have written a base case but the condition to execute it is never satisfied, hence the infinite recursion occurs.

For example, the code of above program 6.4 will face infinite recursion if you enter a negative value for power. In that case, the condition for base case, i.e.,

if  b == 0 :                  #this condition will never be true for a negative value of b

     return 1

Will never be satisfied and hence infinite recursion will occur.

To avoid infinite end recursion, your code should take care of possible values that may cause infinite recursion, e.g., above program (6.4)’s code can be modified as follows to avoid infinite recursion:

  OR

  You may check for negative value of power in_main_ part as well, i.e., as:

You can easily determine the flow of execution in above program.

 

Iterative version of recursion in python

A recursive code may also be written in non-recursive way, which is the iterative version of the same. For instance, the iterative version of above program (6.4)’s code is given in program  6.5 below:

 

Python Code example       

program to calculate a^b using iterative code.

The output produced by above program is as:

 Enter base number: 3
 raised to power of: 4
 3 raised to power of 4 is 81

 

Some Recursive codes

Let us write some python codes that use recursion carrying out its task.

Computing Factorial Recursively in python

Now, consider another example. The factorial of a non-negative number is defined as the product of all the values from 1 to the number:

n! = 1* 2*…*n

It can also be defined recursively as
 

n! = 1                                   if n< 2
      = n*(n -1 ) !                    if n> = 2

Recursively factorial function would be written as follows:

# recursive factorial function 
def factorial (n) :
         if n< 2 :
                 return 1
     return n* factorial ( n-1 )
#_main_
n = int (input (“Enter  number (> 0 ) :” ) )
print (“Factorial of” , n, “is” , factorial (n) )

Sample runs of above program code are:

Enter a number (> 0): 4
Factorial of 4 is 24
=====================
Enter a number (> 0) : 5
Factorial of 5 is 120

       

The iterative version of above given factorial function is ( you already have written this) :

def factorial (n) :
      fact = n
      for I in range (1, n ) :
           fact = fact * I
     return fact

 

Computing GCD recursively in python

We can efficiently compute the god using the following property, which holds for positive integer’s p and q:

  If p > q

The god of p and q is the same as the god of p and p% q. That is, our python code to compute GCD recursively would be:

   Def gcd (p, q ) :
          if q == 0 :
                   return p
      return gcd (q, p%q )

The base case is when q is O, with gcd (p, O ) = p. To see that the reduction step converges to the base case, observe that the second input strictly decreases in each recursive call since p % q < q. If p<q the first recursive call switches the arguments.

Gcd (1440, 408)          

cd (408, 216 )

gcd (216, 24 )

gcd (192, 24 )

gcd (24, 0 )

return 24

return 24

return 24

return 24

return 24

 This recursive solution to the problem of computing the greatest common divisor is known as Euclid’ s algorithm and is one of the oldest known algorithms- it is over 2000 years old.

You can write recursive code for GCD computation yourself. (also refer to solved problem 15 )

 

Fibonacci number in python

You have written program to compute and display Fibonacci series using a loop . Here we are going to develop a recursive method to compute numbers in the Fibonacci sequence. This infinite sequence starts with 0 and 1, which we’ll think of as the zeroth and first Fibonacci numbers, and each succeeding number is the sum of the two preceding Fibonacci numbers. Thus, the third term is 0 + 1 = 1 And to get the fourth term Fibonacci number, we’d sum the 2^nd term (1) and the 3^rd term (1) to get 2. And the fifth term is the sum of the 3^rd term (1) and the 4^th term (2), which is 3.  And so on.

We want to write a method fib that takes some integer n as a parameter and returns the nth Fibonacci number, where we think of the first 1 as the first Fibonacci number. Thus, an invocation of fb (6) should return 8, and the invocation of fib (7) should return 13.

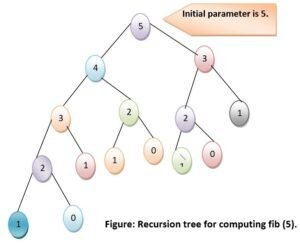
In talking about recursive procedures such as this, it’s useful to be able to diagram the various method calls performed.  We’ll do this a recursion tree. The recursion tree for computing fib (5) is in fig. 6.3.

The recursion tree has the original parameter (5 in this case) at the top, representing the original method invocation. In the case of fib (5), there would be two recursive calls, to fib (4) and fib (3), so we include 4 and 3 in our diagram below 5 and draw a line connecting them. Of course, fib (4) has two recursive calls itself, diagrammed in the recursion tree, as does fib (3). The complete diagram in fig 6.3 depicts all the recursive invocation of fib made in the course of computing fib (5). The bottom of the recursion tree depicts those cases when there are no recursive calls – in this case, when n<= 1.

Following program lists the complete code of using recursive fib ( ) function given above

Python Code example   

program using a recursive function to print Fibonacci series up to nth term.

def fib (n) :
       if n== 1 :        # 1st   term is 0
           return 0
       elif n == 2 :   #  2nd term is 1
           return 1
       else :
           return fb (n – 1 ) + fib (fib (n -2)
#_main_
n = int (input (“Enter last term required :” ) )
for I in range (1, n+ 1 ) :     #list with values 1..n
         print (fib (i), end = ‘ ,  ’)
print (“…..” )

 

The output produced by above program is:

Enter last term required: 8
0, 1, 1, 2, 3, 5, 8, 13 …

 

Binary search in python

Another popular algorithm that uses recursion successfully is binary search algorithm. But hey, we have not talked about binary search before, No worries! We shall first discuss what binary search is, how it works, write its normal iterative code, and then use it recursively too.

Binary search Technique

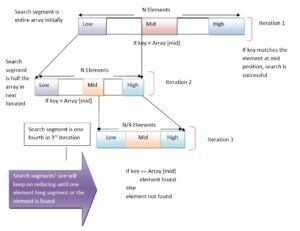
This popular search technique searches the given ITEM in minimum possible comparisons. The binary search requires the array, to be scanned, must be sorted in any order (for instance, say ascending order). In binary search, the ITEM is searched for in a smaller segment (nearly half the previous segment) after every stage. For the first stage, the segment contains the entire array.

To search for ITEM in a sorted array (in ascending order), the ITEM is compared with middle element of the segment (i.e., in the entire array for the first time).if the ITEM is more than the middle element, latter part of the segment becomes new segment to be scanned; if the ITEM is less than the middle element, former part of the segment becomes new segment to be scanned. The same process is repeated for the new segment (s) until either the ITEM is found (search successful) or the segment is reduced to the single element and still the ITEM is not found (search unsuccessful).

Following figure illustrates the process of binary search in a sorted array.

Search item is key in a sorted array with N elements.

Algorithm for Binary search in Linear List (Array AR[ L : U])

Case  I : AR in ascending order

# Initialise segment variables

1. Set beg =, last = u # L is 0, U is size – 1
2. While beg < = last, perform steps 3 to 6
3. Mid = (beg + last )/ 2
4. ifAR [mid] == ITEM then
         {           print (“search successful” )
                     print (ITEM, “found at” , mid )
                     break
          }
5. ifAr [mid] < ITEM then
                  beg = mid + 1
6. ifAR [mid] > ITEM then
                  last = mid -1
   # End of while
7. If beg ≠ last
   print (“unsuccessful search” )

END.

Case II : AR in descending order

# Initialise

:

ifAR [mid] = = ITEM then

{           :

}

ifAR [mid] < ITEM then

last = mid – 1

ifAR[mid] > ITEM then

beg = mid + 1

:

# Rest is similar to the algorithm in case I.

 

Python Code Example

Binary searching in an array (a sorted list)

 

def. binsearch (ar, key ) :

low = 0                                    # initially low end is at 0                                                                                                     

high = len(ar) – 1                     # initially high end is at size – 1

while low < = high :

mid = int ( ( low + high ) / 2 )
if key = = ar [mid] :                             # if key matches the middle element

returned mid                               # then send its inde in array

elif key < ar [mid] :                                                                                

high = mid-1                               # now the segment should be first half

else :

low= mid + 1                              # now the segment should be latter half

else :                                                  # loop’ s else

return- 999

#_main_

Ar = [12, 15, 21,25 28,32,33,36,43,45,]
item= int (input (“Enter search item :”))
res = binsearch (ar, item)
if res > = 0 :                           # if res holds a )0 ..n value

print (item, “FOUND at index”, res 

else :

print (“sorry!” , item, “NOT FOUND in array”)

Some sample runs of the above program as
shown on the right.

Enter search item: 32
32 FOUND at index 5
=====================================
Enter search item: 15
15 FOUND at index 1
=====================================
Enter search item: 10
sorry! 10 NOT FOUND in array
=====================================
 Enter search item: 45
45 FOUND at index 9
======================================
 Enter search item: 12
12 FOUND at index 0
=====================================
 Enter search item: 35
 sorry! 35 NOT FOUND in array

 Pre- requisites of binary search

In order to implement binary search on an array, following conditions must be fulfilled.

1. The given array or sequence must be sorted.
2. Its sort- order and size must be known.

 

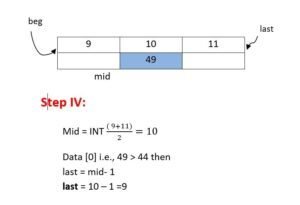
Example:   write the steps to search 44 and 36 using binary search in the following array DATA

 

Solution:

(i) Search for 44.

SEARCH SUCCESFUL At location number 10.

 

(ii) search for 36

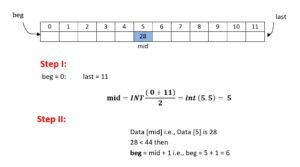
Step I :   beg = 0; last = 11

Mid = INT 

Step II :  Data [mid] i.e., Data [5] is 28
               28 < 36 then beg
                        = mid + 1 = 5 + 1 = 6

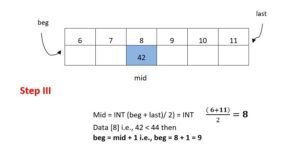
Step III :     mid = INT

                           Data [8] i.e., 42
                           42 > 36 then
                           last =mid – 1 = 8 – 1 = 7

step IV :     mid = INT

                 Data [6] is 31
                    31 < 36 then
                     beg = mid + = 6+ 1 = 7

 

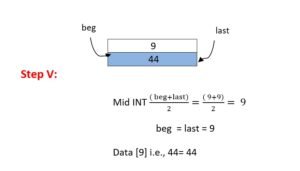
Step V :           mid = INT 

                                               (beg = last = 7)
                          Data [7] is 37    = 37≠ 36

                                    

 SARCH UNSUCCESSFUL!!

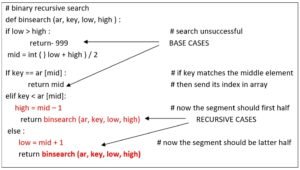
Recursive Binary Search in Python

Now that you have fair idea about Binary search algorithm and how it works, let us see how it can be implemented recursively.

As you can see that process of finding the element is same in all search- segments, only the lower limit low and higher limit high of a segment changes if the element is not found at the middle (mid) position of the search – segment. Thus, a recursive call can be made to the binary search function by changing the limits. The search stops when either the element is found and its index is returned OR lower limit becomes more than higher limit- this will happen when the search- segment reduces to size of single element and search is still unsuccessful, in this case both mid + 1 or mid- 1 will make lower limit more than higher limit- which means search is unsuccessful.

Following program lists the recursive version of binary search algorithm.

Python Code  Example

write a recursive function to implement binary search algorithm.

# _main_
ary = [12, 15, 21,25 28,32,33,36,43,45,]
                                  # sorted array
item= int (input (“Enter search item :”))
res = binsearch (ary, item, 0, len (ary ) – 1))
if res > = 0 :                           # if res holds a 0 ..n value
        print (item, “FOUND at index”, res)
 else :
      print (“sorry!” , item, “NOT FOUND in array”)

 

Some sample runs of the above program as shown below.

Enter search item: 32
32 FOUND at index 5
=====================================
Enter search item: 15
15 FOUND at index 1
=====================================
Enter search item: 10
sorry! 10 NOT FOUND in array
=====================================
 Enter search item: 45
45 FOUND at index 9
======================================
 Enter search item: 12
12 FOUND at index 0
=====================================
 Enter search item: 35
 sorry! 35 NOT FOUND in array

 

Recursion Vs Iteration in Python

Recursion and loops are actually related concepts. Generally, anything you can do with a loop, you can do with recursion, and vice versa. Sometimes one way is simpler to write, and sometimes the other is, but in principal they are interchangeable. Although loop and recursion are interchangeable, yet there are some examples where recursion is indeed the best way to approach a program.

Even for problems that can be treated equally well through iterative and recursion , there is a subtle difference which is because of the way loops and method calls are treated by a programming language compiler.

When a loop repeats, it uses same memory location for variables and repeats the same unit of code. Whereas in recursion, instead of repeating the same unit of code and using the same memory locations for variables, fresh memory space is allocated for each recursive call.

As it happens, any problem that can be solved via iteration can be solved using recursion and any problem that can be solved via recursion can be solved using iteration.

Iteration is preferred by programmers for most recurring events, reserving recursion for instance where the programming solution would be greatly simplified. In a programming language, recursion involves an additional cost in terms of the space used in RAM by each recursive call to a function and in time used by the function call.

Because of extra memory stack manipulation, recursive versions of functions often run slower and use more memory than their iterative counterparts, But this is not always the case, and recursion can sometimes make code easier to understand.

So, you can say that :

• Recursion makes a solution look shorter, closer in spirit to abstract mathematical entity.
• Iterative makes a solution less costly to implement but all logic is part, so lengthier it appears.

It always depends on the problem being solved which approach is better for it – iteration or recursion.