
Number System in Data Representation| CBSE Class 11| Computer Science
Dear Class 11th STUDENTS,
Welcome to this tutorial of Digital Number System from your CBSE class 11 of Computer Science Syllabus .
In this tutorial, we shall be learning our chapter-5 from Unit 1: Computer Systems and Organisation (CSO) as CBSE BOARD suggested to learn about computer system and its organisation to complete this section.
Unit 1: Computer Systems and Organisation (CSO)
Chapter 5: Number System:
- Introduction to number system
- Binary number system
- Octal number system
- Decimal number system
- Hexadecimal number system
- Conversion between number systems
I advice you to check the latest syllabus given by CBSE Board at its Official website: www.cbseacademic.nic.in
Also, in this tutorial we will covers all necessary topics/concepts required to complete your exams preparations in CBSE classes 11th.

NOTE:
- We are also giving some important Questions & Answers for better understanding as well as preparation for your examinations.
- You may also download PDF file of this tutorial from our SHOP for free.
- For your ease and more understanding, we are also giving the video explanation class of each and every topic individually, so that you may clear your topics and get success in your examinations.

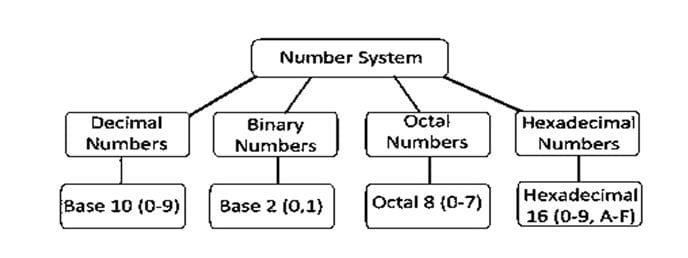
Introduction to Digital Number System in Data Representation
In digital electronics, the number system is used for representing the information. The number system has different bases and the most common of them are the decimal, binary, octal, and hexadecimal. The base or radix of the number system is the total number of the digit used in the number system. Suppose if the number system representing the digit from 0 – 9 then the base of the system is the 10.
Types of Number Systems
Some of the important types of number system are
- Decimal Number System
- Binary Number System
- Octal Number System
- Hexadecimal Number System
These number systems are explained below in details.
Decimal Number Systems
The number system is having digit 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; this number system is known as a decimal number system because total ten digits are involved. The base of the decimal number system is 10.
Binary Number Systems
The modern computers do not process decimal number; they work with another number system known as a binary number system which uses only two digits 0 and1.The base of binary number system is 2 because it has only two digit 0 and 1.The digital electronic equipments are works on the binary number system and hence the decimal number system is converted into binary system.
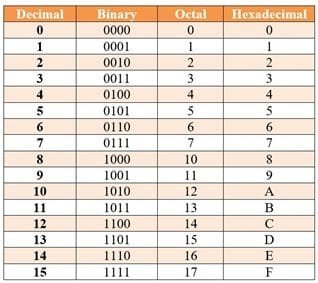
The table is shown below the decimal, binary, octal, and hexadecimal numbers from 0 to 15 and their equivalent binary number.
Octal Numbers
The base of a number system is equal to the number of digits used, i.e., for decimal number system the base is ten while for the binary system the base is two. The octal system has the base of eight as it uses eight digits 0, 1, 2, 3, 4, 5, 6, 7.
All these digits from 0 to 7 have the same physical meaning as by decimal symbols, the next digit in the octal number is represented by 10, 11, 12, which are equivalent to decimal digits 8, 9, 10 respectively. In this way, the octal number 20 will represent the decimal digit and subsequently, 21, 22, 23.. Octal numbers will represent the decimal number digit 17, 18, 19… etc. and so on.
Hexadecimal Numbers
These numbers are used extensively in microprocessor work. The hexadecimal number system has a base of 16, and hence it consists of the following sixteen number of digits.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
The size of the hexadecimal is much shorter than the binary number which makes them easy to write and remember. Let 0000 to 000F representing hexadecimal numbers from zero to fifteen, then 0010, 0011, 0012, etc. Will represent sixteen, seventeen, eighteen… etc. till 001F which represent thirty open and so on.
Conversion between number systems
The binary number system is the most important one in digital systems as it is very easy to implement in circuitry. The decimal system is important because it is universally used to represent quantities outside a digital system.
In addition to binary and decimal, octal and hexadecimal number systems find widespread application in digital systems. These number systems (octal and hexadecimal) provide an efficient means for representing large binary numbers. As we shall see, both these number systems have the advantage that they can be easily converted to and from binary.
In a digital system, three or four of these number systems may be in use at the same time, so that an understanding of the system operation requires the ability to convert from one number system to another. This section discusses how to perform these conversions. So, let us discuss them one by one.
Binary to Decimal Conversion Methods
The decimal number system is represented by the digit 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. It consists ten digits and hence the base of the system is 10. Their base is increased by the factor of 10. On the other hand, the binary number system consists only two digits 1 and 0.The base of the binary number system is 2, and it is increased by the factor of two. The first digit has 20 weights, the second has 21 weights, the weight of the third digit is 22 and so on. Consider a decimal number 3285 it can be written as
3285 = 3000 + 200 + 80 + 5
3285 = 3(103) + 2(102) + 8(101) + 5(100)
Thus the decimal number system is an example of positional notation where each digit position has a weight in terms of powers of ten. Similarly, in the binary number system each digit position has a weight regarding powers of two. Some of the examples of a binary digit are shown in the example.

In binary to decimal conversion when there is one in a digit position of a binary number, then the weight of the position is added. But when there is the zero in a binary position the weight of the position is disregarded.
Considered the conversion of the binary number 10101 into its equivalent decimal numbers
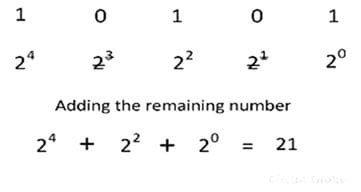
On disregarding the weight 23 and 21 and summing up the remaining weights, we get the equivalent decimal number 21.
Binary to Decimal Conversion for Fractional Number
For a fractional number, the weights of the digit position to the right of binary point are given by 2-1, 2-2, 2-3, 2-4… etc. Consider the conversion of a fractional binary number.0101 into its equivalent decimal numbers.
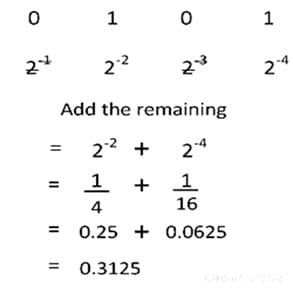
Binary to Decimal Conversion For Mixed Number
The number with an integer and fractional part are called mixed number. The weight for a mixed number can be written as
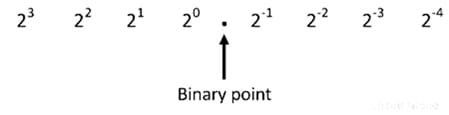
Consider the conversion of a binary number 1101.101 into its equivalents decimal number
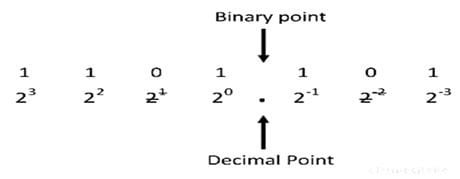
After disregarding the weight 21 and 2-1 and on summing up the remaining weights the required decimal number is 13.625.
Hexadecimal to Binary & Binary to Hexadecimal Conversion Methods
The hexadecimal numbers are mostly used in microprocessor work. The base of the hexadecimal number is 16 and its consist the number from 0 -15. It uses the number system from 0-9 and then represents by the alphabets from A- F. The hexadecimal number system is also called hex. It is one of the convenient ways of describing the binary digit number. The large binary digits are easily represented by the hexadecimal number.
The base of the binary number system is two because it is represented by two digits, i.e., 0 and 1. It is difficult to represent the large number in the form of binary digit and hence the hexadecimal systems are used in the digital electronics.The hexadecimal number systems are easily converted into a binary system by using the method explains below.
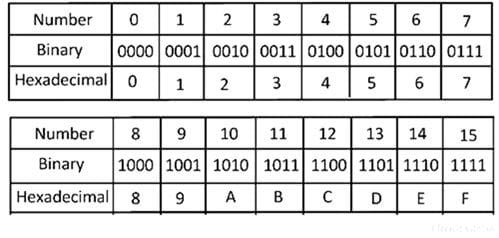
Hexadecimal to Binary Conversion Method
To convert a hexadecimal number to a binary number, convert each hexadecimal digit to its four digit equivalent. For example, consider the hexadecimal number 9AF which is converted into a binary digit. The conversions are explained below.
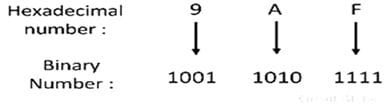
Therefore the equivalent binary number is 1001 1010 1111.
Binary to Hexadecimal Conversion Methods
To convert the given binary number into its equivalent hexadecimal number rewrite the binary number of the sets of four digits and then place the hexadecimal digit in front of each four digit set of a binary number as explained by the following number.
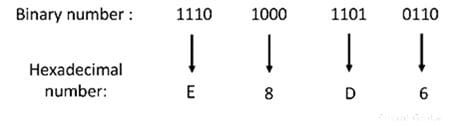
Thus the equivalent hexadecimal number is E8D6.
Octal to Decimal & Decimal to Octal Number Conversion
Definition: The number system whose base is 8 is known as the octal number system. The base 8 means the system uses eight digits from 0 to 7. All the eight digits from 0 to 8 have same physical meaning as that of decimal numbers. The next digit in octal number is represented by 10, 11, 12, 13, 14, 15, 16, 17 which represents the decimal digits 8, 9, 10, 11, 12, 13, 14, 15. In this manner the octal number 20 represents the decimal number 16 and subsequently 21, 22, 23….octal numbers will show the decimal digits 17, 18, 19… etc and so on.
The major disadvantage of the octal number system is that the computer doesn’t understand the octal number system. So the additional circuit is required for the digital systems which convert the octal number to binary number. The octal number system is used in a minicomputer.
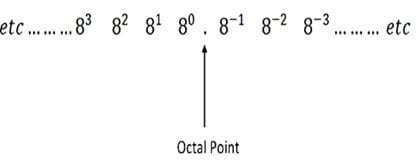
Octal to Decimal Number Conversion
In octal number system, each digit position has the weight eight regarding power eight shown in the figure below.
Decimal to Octal Number Conversion
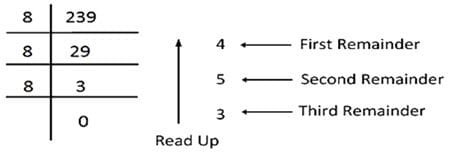
For converting the decimal number into an octal number, the octal dabble method is used. In the octal double method, the integer octal number is divided by the digit 8. And for converting the fractional decimal number into an octal number, it is multiplied by the digit 8 and record the carry. When these carry read down, it gives the fractional octal number.
Example: Consider the conversion of the decimal number 236.53. The conversion of integer part is shown below.
And the for the remaining fraction part

Hence, the octal number is 354.4172.
Octal to Binary & Binary to Octal Conversion Methods
The base of the octal number system is 8 because it consists the digit from 0 – 7. The octal number system is converting into binary number system by grouping the binary digit in the group of three from the right of the binary number. On the other hand, the base of the binary digit is 2 and it consists only two digits 0 and 1. The octal number can easily be converted into binary by the help of the method explained below.
Octal to Binary Conversion
The base of the octal number system (8) is the third power of base of a binary system (2), the inter conversion of octal and a binary number is very simple and direct as explained below.
Let converting the octal number 35.346 to its equivalent binary number
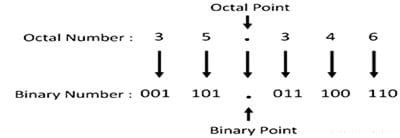
Thus the required binary number is 011 101. 011 100 110.
Binary to Octal Conversion
The conversion of binary to octal is a reversal of the above procedure. For example, the binary number 010100111.100011 can be converted into an octal number by first written the bits in the group of three and then awarding the decimal number of to each of the group of three bits as shown below.
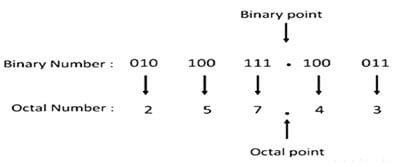
Thus the required octal number is 257.43
Alternate Method of Octal to Binary Conversion
In this method, the large decimal number is first converted into an octal number and then to a binary number instead of direct conversion of decimal to binary number as shown in the following examples.
Suppose it is required to convert the decimal number 465 into a binary number. Let us find an octal number of 465 using the octal dabble method.
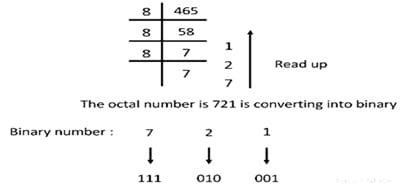
Hexadecimal to Decimal & Decimal to Hexadecimal Conversion Methods
The decimal number system has 10 digits from 0 – 9 and hence the base of the system is 10. On the other hand, the hexadecimal number system has 16 digits. The base of the hexadecimal number system is 16. The first 10 digits are expressed by the number and the remaining digits are represented by the alphabets. The value of the decimal number system depends on the location of the digit and the decimal points represent the fractions.
Hexadecimal to Decimal Conversion Method
The base of the hexadecimal number system is 16, therefore the weights corresponding to various positions of the digits will be as shown below.
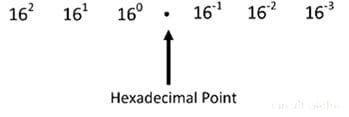
For an instance, consider the conversion of hexadecimal number E8F6.27 into its equivalent binary number.
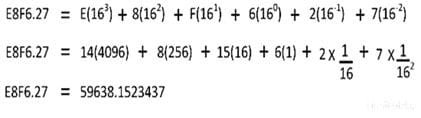
Decimal to Hexadecimal Conversion Method
The conversion of the given decimal number into hexadecimal number requires the application of hex-dabble method which is similar to the double-dabble method with the exception that one has to divide the given number by 16 instead of 2.
Consider the conversion of the decimal number 3749 into its hexadecimal equivalent number.
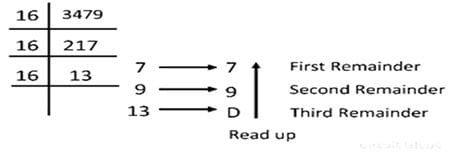
The third reminder 13 is equivalent to D in a hexadecimal number system. Thus the equivalent hexadecimal number D97


