Computational Thinking & Problem Solving in Python | CBSE Class 11| Computer Science

Dear Class 11^th STUDENTS !, Welcome to this tutorial of Computational Thinking & problem Solving in python from your CBSE class 11 of Computer Science Syllabus .

In this tutorial, we shall be learning our chapter-1: Computational Thinking & problem Solving in python from Unit 2: Computational Thinking & programming-1 as CBSE BOARD suggested to learn about computational thinking and problem solving with programming to complete this section.

Unit 2: Computational Thinking & programming-1    

Chapter 1: Computational Thinking & problem Solving in python:

• INTRODUCTION.
• STEPS IN PROBLEM SOLVING CYCLE.
  • Analyzing the problem,
  • Developing an algorithm,
  • Coding,
  • Testing, and
  • Debugging
• PROBLEM SOLVING USING DECOMPOSITION.
• NEED FOR DECOMPOSITION.
• DESIGNING ALGORITHMS.
• CHARACTERSTICS OF A GOOD ALGORITHM.
• COMPONENTS OF AN ALGORITHM.
• FLOWCHART.
• PSEUDOCODE.
• SOME IMPORTANT QUESTIONS.

I advice you to check the latest syllabus given by CBSE Board at its Official website: www.cbseacademic.nic.in

Also, in this tutorial we will covers all necessary topics/concepts required to complete your exams preparations in CBSE  classes 11th.

NOTE:

• We are also giving some important Questions & Answers for better understanding as well as preparation for your examinations.
• You may also download PDF file of this tutorial from our SHOP for free.
• For your ease and more understanding, we are also giving the video explanation class of each and every topic individually, so that you may clear your topics and get success in your examinations.

INTRODUCTION TO COMPUTATIONAL THINKING

Computational Thinking is a systematic approach to solving problems, involving breaking them down, identifying patterns, abstracting details, and developing algorithms. In CBSE Class 11, this is applied through the study of Python programming, where these concepts are translated into code to solve problems. 

There is a famous quote by Steve Jobs, which says, “Everyone in this country should learn to program a computer, because it teaches you to think”.

This quote itself is proof-enough to say that in order to program a solution for a problem, you should think in a specific way. And this is what we are going to talk about in this tutorial. In this chapter, you will learn about problem solving, i.e., analyzing a problem, designing algorithms using tools like flowcharts and pseudocode and problem-solving using decomposition.

So, let us begin.

Key aspects of Computational Thinking:

• Decomposition: Breaking down a complex problem into smaller, more manageable parts. 
• Pattern Recognition: Identifying similarities, patterns, and trends in data. 
• Abstraction: Focusing on relevant information while ignoring unnecessary details. 
• Algorithm Design: Developing step-by-step instructions to solve the problem. 

How to apply computational thinking in Python:

• Understand the problem: Clearly define the problem and its requirements. 
• Decompose the problem: Break it down into smaller, more manageable subproblems. 
• Develop an algorithm: Create a step-by-step solution for each subproblem. 
• Represent data: Use appropriate data structures (like lists, dictionaries, etc.) to represent the data. 
• Implement the algorithm in Python: Write the code to execute the algorithm using Python. 
• Test and refine: Test the code, identify and fix any errors, and refine the algorithm for better performance. 

Problem Solving in Python:

• Problem Definition: Clearly define the problem you want to solve. 
• Algorithm Design: Create an algorithm (a set of steps) to solve the problem. This can be represented in natural language, as a flowchart, or through pseudocode. 
• Coding: Translate the algorithm into Python code. 
• Testing and Debugging: Test the code to ensure it works correctly and fix any errors. 

Benefits of Computational Thinking:

• Improved Problem-Solving Skills: Develops systematic thinking and problem-solving abilities. 
• Enhanced Programming Skills: Provides a foundation for understanding and using programming languages like Python. 
• Increased Creativity: Encourages innovative solutions to problems. 
• Transferable Skills: The principles of computational thinking are valuable across various disciplines. 

Examples of Computational Thinking & Problem Solving:

Example1:

Let’s say you want to write a Python program to calculate the area of a triangle.

• Decomposition: You break down the problem into smaller parts: inputting the base and height, applying the area formula, and outputting the result. 
• Pattern Recognition: You recognize that the area of a triangle is always (1/2) * base * height. 
• Abstraction: You ignore the specific dimensions of the triangle and focus on the general formula. 
• Algorithm Design: You write the steps:

• Get the base as input.
• Get the height as input.
• Calculate the area (1/2 * base * height).
• Print the result.

• Coding: You translate this into a Python program. 

def triangle_area():
base = float(input(“Enter the base: “))
height = float(input(“Enter the height: “))
area = 0.5 * base * height
print(“The area is:“, area)

triangle_area()

Example2:

STEPS IN PROBLEM SOLVING CYCLE

Programs are not quick creations. In order to create efficient and effective programs, you should adopt a proper problem-solving methodology and use appropriate techniques. In fact, problem solving methods follow a cycle and this cycle is called The Problem-Solving Cycle. In this tutorial, we are going to discuss this Problem-Solving Cycle.

Broadly problem solving requires four main steps:

1. Identify and analyze the problem.
2. Find its solution and Develop algorithm of the solution.
3. Code the solution in a programming language.
4. Test and Debug the coded solution.

And finally implement and maintain it.

The above-mentioned steps are four major steps in a problem-solving cycle. Each step contains many sub-steps.

Let us talk about these sub-steps in order to understand the problem-solving cycle. The aim of a problem-solving cycle is to create a working program for the solution.

The sub-steps of a problem-solving cycle to create a working program are:

Analyze the problem

Understand the problem well

It is very important to understand the problem minutely because sometimes the problem is not that appears but something else the is causing it.

Analyze the problem

Problem analysis is very important as the outcome of this will convert to the success of final solution. While analyzing

• identify processing components
• identify the relationships among processing components.

Developing the Algorithm

Think of possible solutions

As per the problem analysis, think of possible solutions by trying this: think of different ideas for solutions

• Think of different ideas for solutions.
• Check your ideas for aptness.
• finally, zero on most appropriate solution.

 Follow Modular approach while designing most appropriate solution

Many small logically related modules or functions must be preferred over a big problem. It is called Modular approach wherein we divide a big program into many smaller and more understandable modules.

Design the final program by

• deciding step by step solution
• breaking down solution into simple steps.

 Identify operations for solution

Program coding involves identification of constituent opera-b required to get the desired output. One must decide about the minimum but simple operations required. Identify:

• Minimum number of inputs required
• Arithmetic and logical operations required for solutions
• Simple and efficient data structures suiting the need.

Coding

Code program using appropriate control structures

The next step is to code the program as per finding of previous step. Coding is the technical word for writing the program. This step is to translate the algorithm into a programming language. You should use most appropriate control structures out of available options. Thus, it is important to know the working of different control structures and their suitability in different situations.

• Use appropriate control structures such as conditional or looping control structures.
• Think program’s efficiency in terms of speed, performance and effectiveness.

Testing and Debugging

Test and Debug your Program

Testing is the process of finding errors in a program and debugging is the process of correcting errors found during the testing process. Thus, this phase involves:

• Finding errors in it.
• Rectifying the errors.

Complete your documentation

Documentation is intended to allow another person or the programmer at later date, to understand the program. Documentation might also consist of a detailed description of what the program does and how to use the program.

Implement and Maintain

Implement your code

After testing and documentation, implement your program for actual use on site. Now, the real users can use your programs.

Maintain your program

Maintaining programs involves modifying the programs to remove previously undetected errors, to enhance the program with different features or functionality, or keep the program up-to-date as government regulations or company policies change.

PROBLEM SOLVING USING DECOMPOSITION

In previous section we talked about problem solving cycle. The first five steps of problem-solving cycle are very important as rest of the steps are based on them.

The first five steps involve understanding the problem, analyzing it, and thinking of possible solution with sub-module and operations in it. All this is effectively carried out using decomposition. Let us know what decomposition means.

Decomposition is the process of breaking down a big or complex problem into a set of smaller sub-processes in order to understand a problem or situation better, is known as decomposition.

It is the process of breaking down a big or complex problem into a set of smaller sub-processes to allow us to describe, understand, or execute the problem better. Decomposition involves:

• Dividing a task into a sequence of subtasks.
• Identifying elements or parts of a complex system.

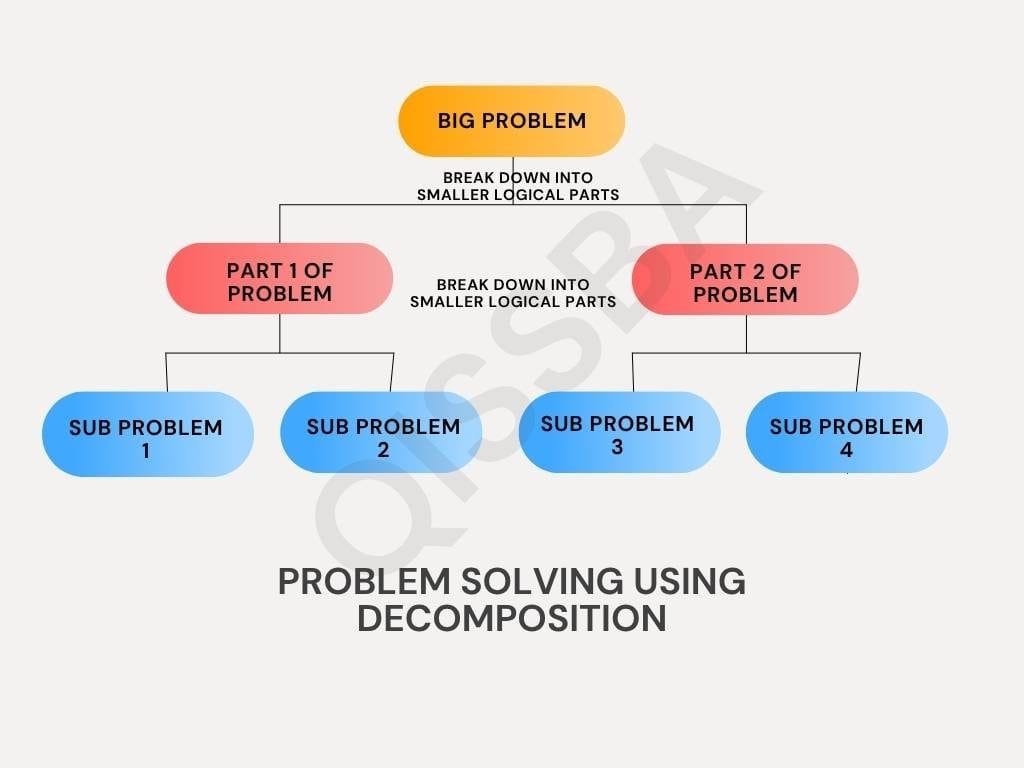
Consider some examples of decomposition:

Everyday example: Making cookies is a complex task that can be broken down into smaller, simpler tasks such as mixing up the dough, forming into shapes via cookie cutters, and baking.

Academic example: Writing an essay is a complex task that can be broken down into smaller tasks such as developing a thesis, gathering evidence, and creating a bibliography page.

Engineering example: Designing a solution to construct a bridge by considering site conditions, technology available, technical capability of the contractor, foundation, etc.

Computer Science example: Writing a computer program/software by determining a well-defined series of smaller steps (mostly in the form of modules and functions) to solve the problem or achieve a desired outcome.

NEED FOR DECOMPOSITION

Decomposition is the process of breaking a large problem into more manageable sub-problems. It is very important to decompose a problem into smaller sub-problems, reason being that large problems are disproportionately harder to solve than smaller problems. It’s much easier to write two 500-line programs than a single 1000-line program. Larger a problem is, harder and more difficult it is to program as compared to a smaller problem.

Once you know how decompose a problem in smaller steps, you can create its solution by designing algorithm for it.

DESIGNING ALGORITHMS

Computers are essentially problem-solving devices. Computers solve these problems by dividing the problems in simple and small steps that are expressed in the form of computer instructions.

The set of rules that define how a particular problem can be solved in finite number of steps is known as algorithm. An algorithm is composed of a finite set of steps, each of which may require one or more operations. But there are certain constraints to be placed on the type of operations as algorithm can include.

These are:

• Each operation must be definite

it must be clearly defined what should be done. For instance, ‘x=6/0, ‘add 3 or 8 to a’ are not permitted as these operations are not clearly defined.

• Each operation must be effective

each step must be such that it can be done using pencil and paper in a finite amount of time. For example, arithmetic on integers is effective operation, whereas arithmetic on real numbers is not since some values may be expressible only by an infinitely long decimal expansion.

• Each operation must be finite

the algorithm should terminate after a finite number of operations.

Thus, we can say that a good algorithm must have characteristics as listed in the following

Characteristics of a Good Algorithm

In order to be an effective algorithm, an algorithm must have the following characteristics:

1. Precision: An algorithm should be precise, i.e., its steps should be precisely defined.
2. Uniqueness: Every step should uniquely contribute to the algorithm. It means that the result of a step is unique and it is only dependent on the input and the result of the preceding steps.
3. Finiteness: An algorithm must be finite. It must not repeat the steps endlessly. The algorithm must stop after a finite number of instructions have been executed.
4. Input: An algorithm requires a specific type of input to work upon.
5. Output: An algorithm produces output as per the stated objectives and the input it has received.

Components of an Algorithm

An algorithm clearly identifies the following components:

Input – the inputs and the type of inputs required by the algorithm. The inputs can be provided by a user or can be self-obtained too, such as reading from a file.

Processing – what and how the processing would use inputs to produce the desired output.

Output – the output expected from the algorithm; the objective of the algorithm.

A program is the expression of an algorithm in a programming language. Thus, the success of a program depends upon the algorithm. Therefore, the logic of the problem must be clearly expressed in algorithm. The logic of the problem can be expressed in various manners. One of the most preferred methods is the graphical method of representing the problem’s solution, which is known as flowchart.

Another useful tool for designing algorithms is pseudo-code. In the coming subsections, we are talking about both these tools.

FLOWCHART

The flowchart is a graphical representation of an algorithm. A flowchart shows different subtasks with different symbols. following figure shows commonly used flowchart symbols.

With flowchart, a programmer can pictorially view the subtasks of an algorithm and the order their execution.

A flowchart is a pictorial representation of step by step solution of a problem. For example.

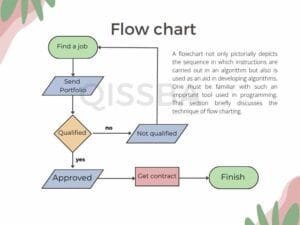
A flowchart not only pictorially depicts the sequence in which instructions are carried out in an algorithm but also is used as an aid in developing algorithms. One must be familiar with such an important tool used in programming. This section briefly discusses the technique of flow charting.

There are various flowchart symbols that carry different messages and are used for different purposes. These symbols are shown below:

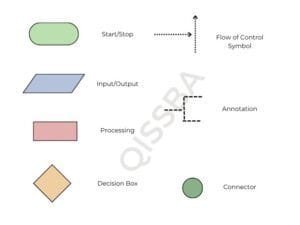
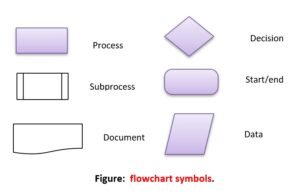
• Data symbol for input /Output (I/O) operation (taking input and showing output).
• Process symbol for any type of computation and internal operations like initialization, calculation etc.
• Subprocess symbol to invoke a procedure written already.

 The flowchart for the above algorithm

Determine if the first number is divisible by second number or not will be:

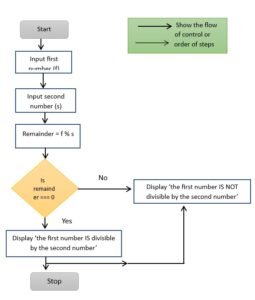
Following section illustrates the working and use of flow charts along with algorithm development.

Writing Algorithms

To write algorithms, such a language should be used that is close enough to the programming language(s) (in which the programs are to be written) so that a hand translation is relatively easy to accomplish. Thus, we have chosen a language for algorithms that resembles our programming language Python.

Let us discuss certain rules for writing algorithms.

Identifiers

Identifiers are the names given to various components of a program by the programmer e.g., to variables that hold values, to functions, modules etc.

While choosing names for identifiers, make sure that these are meaningful and not unnecessarily long or short names.

Assignment

The assignment of values to variables is done through assignment statement as :

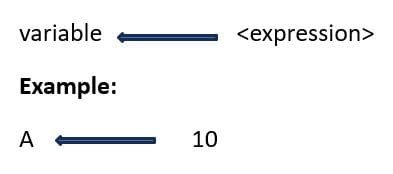
In an algorithm, the left arrow (+-) denotes the act of assigning the value of its right-hand side to the variable on its left. Some people take liberty and use assignment operator to assign values to variables in algorithms.

Sequence

The steps of an algorithm are executed in the sequence of top to bottom. One after another so steps must be listed in the correct order.

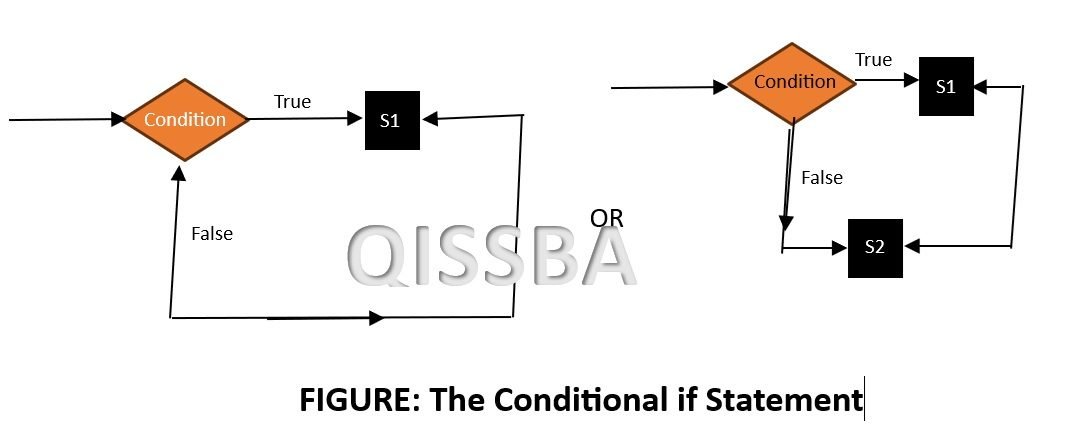
Selection/Conditional Statements

A conditional statement in an algorithm takes the following form:

There may be one or more if-then-else statements embedded in another if-then-else statement. Above figure depicts conditional statements pictorially.

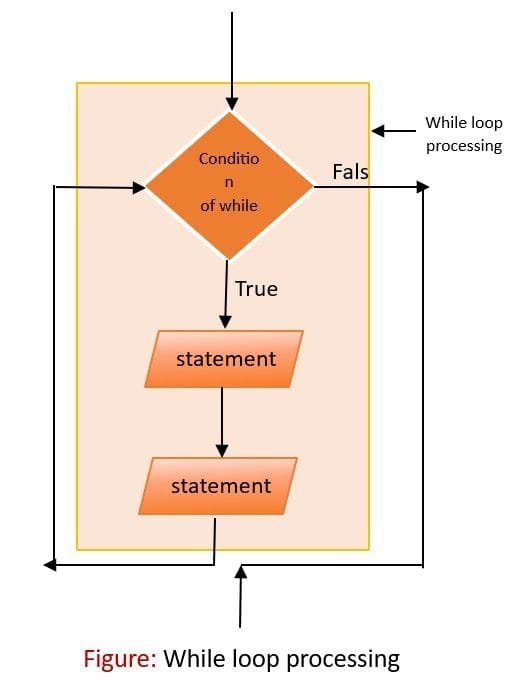
Repetition Looping Statement

A looping statement (also called iteration statement) lets you repeat a set of statements depending upon a condition. To accomplish iteration, the for loop and while loop are used.

for looping statement

for item in sequence:

       : St             #block of statements

:

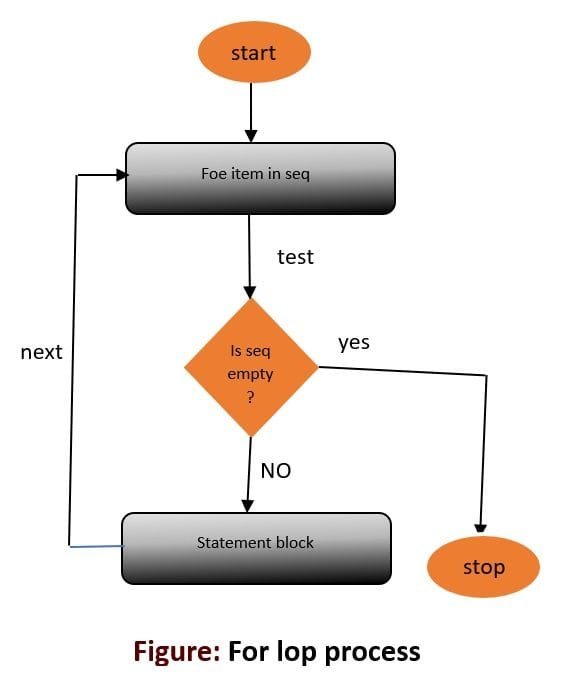
St represents the set of statements to be repeated for each item in the sequence. When the statements block gets executed for each item in the sequence, the for-loop stops.

while looping statement

while condition:

         : St              #block of statements

    :

St represents the set of statements to be repeated. The while iteration statement tests the condition before entering into the loop. Thus, if the condition is false even before entering into the loop, the while-loop will never get executed.

PSUEDOCODE

Pseudocode is an informal language that helps programmers describe steps of a solution without using any programming language syntax. Pseudocode is a “text-based” detail (algorithmic) design tool. A pseudocode creates an outline or a rough draft of a program that gives the idea of how the algorithm works and how the control flows from one step to another.

For example, consider the following pseudocode:

If student’s marks is greater than or equal to 50 display “passed”

else

display “failed”

The above pseudocode gives you an idea how a program determines whether a student has passed or failed comparing the marks of the student.

Consider the same algorithm that we talked in example 5 (determine if the first number is greater than the second number or not). The pseudocode of this algorithm can be like:

Input first number in variable firstnum.

Input second number in variable secondnum

if the firstnum is > the secondnum

else

display ‘the first number IS greater than second number*.

display ‘the first number IS greater than second number’.

Please note there are no standard rules to write a pseudocode as it is totally informal way of representing an algorithm.

Advantages and Disadvantages of Pseudocode

The pseudocode is a very useful and helpful tool in algorithm development. It offers many advantages and it has some disadvantages too.

Pseudo-code Advantages

• It uses a language similar to everyday English, thus is easy to understand.
• It highlights the sequence of instructions.
• The structure of an algorithm is clearly visible through pseudocode, e.g., selection and repetition blocks.
• Pseudocode can be easily modified without worrying about any dependencies.

Pseudo-code Disadvantages

• It is not a visual tool like flowcharts.
• Since there is no accepted standard for pseudocode, so it varies from programmer to programmer.
• It can only be tested on paper, there is no program available to test it.
• It is an informal representation of an algorithm.

SOME IMPORTANT QUESTIONS

Here is a snap of some important questions asked in CBSE Class 11 & 12th examinations.

• What are the 4 concepts of computational thinking?
• What are the 4 stages of computational thinking?
• What are the 5 steps of computational thinking?
• What is the meaning of computational in computer?
• Discuss about the building blocks of an algorithm 
• Explain the steps to identify the computational problem 
• Explain the iteration method for developing an algorithm 
• Write a recursive algorithm of tower of Hanoi
• Discuss about the building blocks of an algorithm 
• Explain the steps to identify the computational problem 
• Identify the simple strategies for developing an algorithm 
• Write an algorithm to insert a card into a list of sorted cards

To read more for Class 11th Computer Science

Python Full Course for Beginners | Complete All-in-One Guide | CBSE Class 11